lunes, 9 de mayo de 2011

3.7 transformada de funciones multiplicativas

Sea f una función compleja definida en la recta e integrable con respecto a la medida de lebesgue, en símbolos,
f \in L^1(\mathbb{R}).
La transformada de Fourier de f es la función
\hat{f}(\xi ) = \frac{1}\sqrt{2\pi} \int_{-\infty}^{+\infty} f(x)e^{-i\xi\,x} dx
Esta integral tiene sentido, pues el integrando es una función integrable. Una estimativa simple demuestra que la transformada de Fourier F(f) es una función acotada. Además por medio del teorema de convergencia dominada puede demostrarse que F(f) es continua.
La transformada de Fourier inversa de una función integrable f está definida por:
\check{f}(\xi ) = \frac{1}\sqrt{2\pi} \int_{-\infty}^{+\infty} f(x)e^{i\xi\,x} dx
Nótese que la única diferencia entre la transformada de Fourier y la transformada de Fourier inversa es el signo negativo en el exponente del integrando. El teorema de inversión de Fourier formulado abajo justifica el nombre de transformada de Fourier inversa dado a esta transformada.
Publicado por en

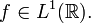
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)