Siendo
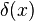 para el caso
para el caso 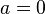
En física, la delta de Dirac puede representar la distribución de densidad de una masa unidad concentrada en un punto a. Esta función constituye una aproximación muy útil para funciones picudas y constituye el mismo tipo de abstracción matemática que una carga o masa puntual. En ocasiones se denomina también función de impulso. Además, la delta de Dirac permite definir la derivada generalizada de funciones discontinuas. Concretamente, se tiene la siguiente relación con la función escalón:
Intuitivamente se puede imaginar la función δ(x) como una función que tiene un valor infinito en x = 0; tiene un valor nulo en cualquier otro punto, de tal manera que su integral es uno.
Estas propiedades se pueden demostrar multiplicando ambos miembros de cada igualdad por una función f(x) e integrando teniendo en cuenta que la función delta no puede formar parte del resultado a menos que esté dentro de una integral.
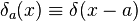
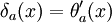
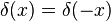
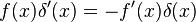

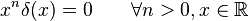
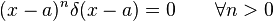

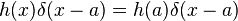
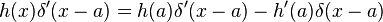

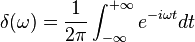

No hay comentarios:
Publicar un comentario